Numerical modeling of interphases with applications to structural adhesive components
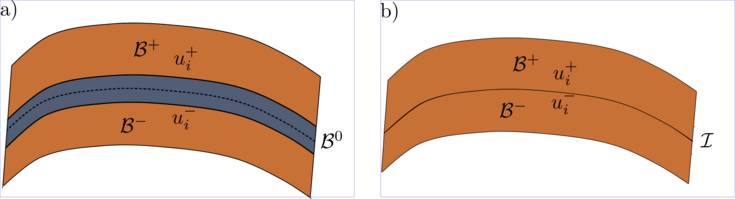
Figure 1: a) Interphase B0 between bodies on top B+ and bottom B-. b) Equivalent interface.
Our research project research focuses on the modeling of interphases and the development of generalized interface models. Interphases are ubiquitous in nature across all scales and occur as transition zones between different materials. Inside these transition zones a multitude of physical phenomena develop giving rise to the overall mechanical behavior of the adhesive structural bond. Incorporating all these phenomena to a numerical simulation is a challenging task. Moreover, since the thickness of the interphase is much smaller than the dimensions of the rest of the structural bond components it often leads to using prohibitively large amount of computational resources. In order to correctly account for the physics of the interphase at larger scales homogenized models have been proposed. These models aim at replacing the interphase with an equivalent interface significantly reducing the computational cost see Figure 1 and [1,4,5]. However, with the exception of special cases [2,3] these models are mostly contained within the framework of linear elasticity which restricts their use in more general applications such as the bonding of structural components.
Our research goals therefore, are to:
- Assess the capabilities of the different approaches in deriving equivalent generalized interface models for the numerical modeling of structural bonding components.
- Extending the models to the general case involving non linearities such as (visco)-plasticity, damage and large deformation.
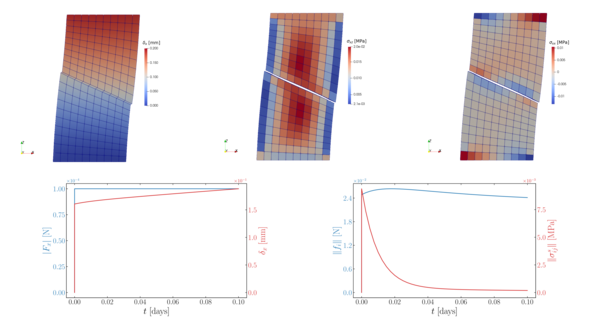
Going beyond already established research we investigate the behavior of generalized interface modes in the case linear viscoelastic interphases. In this case the original features of the generalized interface model (i.e displacement jump, stress discontinuity,surface elasticity) are enhanced by the time dependent characteristics of the viscous contribution.
In particular we show in Figure 2 the viscoelastic behavior of a three-body system comprising of two elastic bodies on top and bottom and a viscoelastic interface layer. The three body system is subjected to a creep test by application of a constant nodal force on the top surface. We observe the viscous behavior developing on the displacement response of the top surface. We also observe the formation of a displacement jump due to the lower elasticity of the interphase layer. Moreover, we note the interplay of the viscous force due to the displacement jump and surface stress due to the surface viscoelasticity of the interphase layer.
References:
[1] Benveniste, Y., & Miloh, T. (2001). Imperfect soft and stiff interfaces in two-dimensional elasticity. Mechanics of materials, 33(6), 309-323.
[2] Costanzo, F. (1998). A continuum theory of cohesive zone models: deformation and constitutive equations. International Journal of Engineering Science, 36(15), 1763-1792.
[3] Gu, S. T., Liu, J. T., & He, Q. C. (2014). The strong and weak forms of a general imperfect interface model for linear coupled multifield phenomena. International Journal of Engineering Science, 85, 31-46.
[4] Javili, A. (2018). Variational formulation of generalized interfaces for finite deformation elasticity. Mathematics and Mechanics of Solids, 23(9), 1303-1322.
