Constitutive Modeling of Anisotropic Quasi-Brittle Materials
Quasi-brittle materials exhibit a complex mechanical behavior characterized by:
- an initial linear elastic response, followed by
- a plastic response with strain hardening up to the peak strength,
- strain softening accompanied by a degradation of material stiffness, and
- a dependency on hydrostatic pressure,
as illustrated in Figure 1.
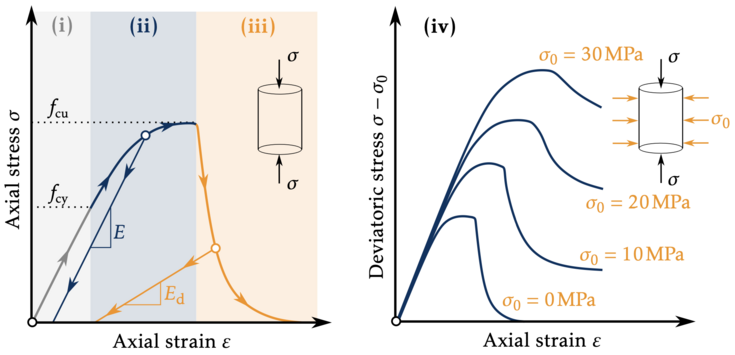
Figure 1: Idealized stress-strain curves of quasi-brittle materials under uniaxial compression (left) and triaxial compression with different confining pressures σ0 (right).
In addition, natural materials such as intact rock and rock mass or additively
manufactured materials such as 3D printed concrete exhibit a layered structure, significantly influencing the mechanical behavior by directional dependencies. These dependencies can be classified into:
- inherent anisotropy, arising from the micro- and macrostructure of the material, and
- induced anisotropy, resulting from damage processes, such as crack orientation.
The objective of this research is to develop a mathematical framework that accurately describes this complex mechanical behavior, incorporating both the aforementioned nonlinearities and the directional dependencies induced by the layering. Particular emphasis is placed on ensuring a robust and stable formulation of the material models, making them suitable for large-scale finite element simulations. To achieve mesh-independent results, special attention is given to the regularization of the softening regime.
In Mader et al. [1] a transversely isotropic damage plasticity model for layered rock and rock mass has been introduced, which was validated by triaxial compression tests on Tournemire shale (see Figure 2).
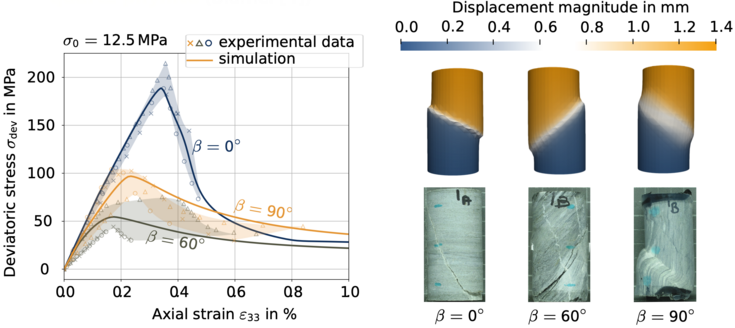
Figure 2: Comparison of the computed deviatoric stress – strain curves to experimental data (left) and the corresponding failure modes (right) for different loading angles with respect to the layering.
Furthermore, the model was successfully applied to numerical simulations of tunnel excavation in Mader et al. [2]. These simulations highlight the significant influence of directional dependencies of the surrounding rock mass on the deformation pattern of the tunnel cross section (see Figure 3).
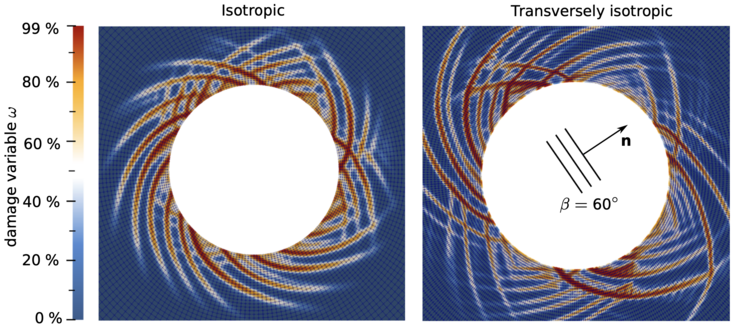
Figure 3: Comparison of the computed damage pattern of the surrounding rock mass of a tunnel cross section considering isotropic (left) and transversely isotropic behavior due to the layering (right).
For modeling the orthotropic mechanical behavior induced by the printing process of 3D printed concrete, an orthotropic damage plasticity model was proposed in Mader et al. [3]. Figure 4 illustrates the influence of layering on a 3D printed arch structure, emphasizing the importance of considering direction-dependent mechanical behavior in numerical simulations of 3D printed concrete structures.
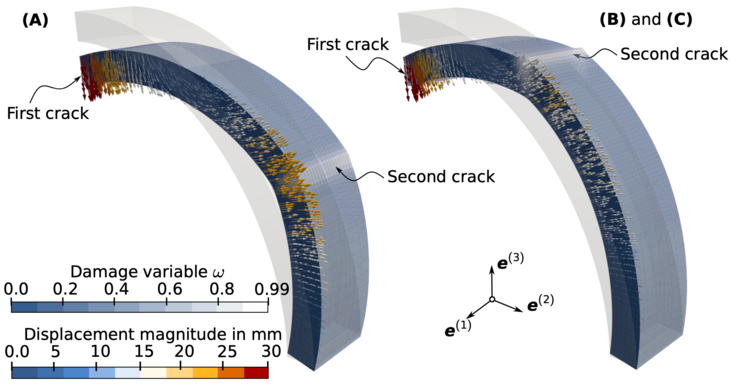
Figure 4: Comparison of the computed failure modes of a 3D printed arch structure with different orientations of the printing layers (cf. Mader et al.[3]).
[1] T. Mader, M. Schreter, and G. Hofstetter (2022a). “A gradient enhanced transversely isotropic damage plasticity model for rock - formulation and comparison of different approaches”. In: International Journal for Numerical and Analytical Methods in Geomechanics 46 (5), pp. 933–960.
[2] T. Mader, M. Schreter, and G. Hofstetter (2022b). “On the Influence of Direction-Dependent Behavior of Rock Mass in Simulations of Deep Tunneling Using a Novel Gradient-Enhanced Transversely Isotropic Damage–Plasticity Model”. In: Applied Sciences 12 (17 - Special Issue: Structural Mechanics of Rocks and Rock Masses), p. 8532.
[3] T. Mader, M. Schreter-Fleischhacker, O. Shkundalova, M. Neuner, and G. Hofstetter (2023). “Constitutive Modeling of Orthotropic Nonlinear Mechanical Behavior of Hardened 3D Printed Concrete”. In: Acta Mechanica 234, pp. 5893-5918
