Enhancing Meshfree Particle Methods
Enhancing Meshfree Particle Methods for Large Deformation Analysis in Generalized Continua
Describing quasi-brittle material failure is a challenging task in computational mechanics. While classical continuum models – usually based on softening plasticity, damage mechanics, or their combination – are basically able to represent such failure, they suffer from a lack of objectivity, leading to the loss of ellipticity in the governing differential equations. This, in turn, causes strain localization to the smallest possible entity, typically a single row of elements in finite element simulations, resulting in mesh sensitivity and non-convergent numerical behavior.
To ensure a stable and robust material model formulation, an appropriate regularization method is necessary to overcome these issues and achieve mesh-insensitive results in numerical simulations. Generalized continua, such as gradient-enhanced, Cosserat, or micromorphic continua, have proven to be effective in regularizing the previously mentioned issues in the softening regime (see Figure 1).
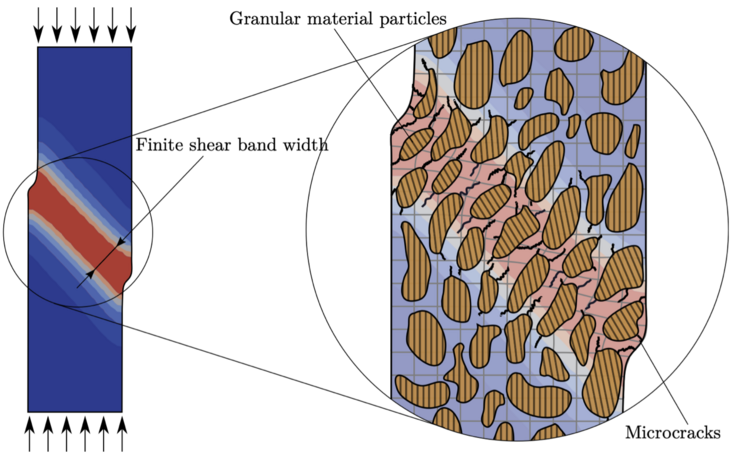
Figure 1: Computed shear band of a quasi-brittle material using a finite strain gradient-enhanced micropolar damage-plasticity model (cf. Neuner, et al. [1]).
However, such localized failure behavior inherently leads to large deformations in the failure zone, causing excessive mesh distortions when using Lagrangian finite element methods (see Figure 2).
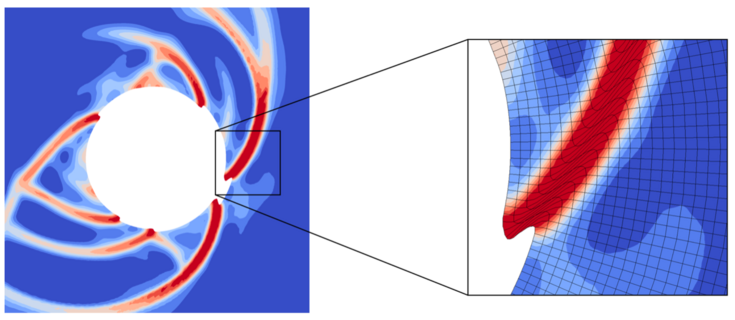
Figure 2: Computed damage distribution of borehole breakout, using a finite strain gradient-enhanced micropolar damage-plasticity model for sandstone within the classical finite element method (cf. Neuner et al. [2]).
Meshfree particle methods, such as the Particle Finite Element Method (PFEM), Discrete Element Method (DEM), Smoothed Particle Hydrodynamics (SPH), Reproducing Kernel Particle Method (RKPM), and the Material Point Method (MPM), have proven to be suitable alternatives for solving large deformation problems.
Recently, Neuner et al. [3] successfully applied a B-spline-based implicit MPM to generalized continua for modeling large localized deformations. Unlike Lagrangian finite elements, MPM discretizes the geometry using particles that move freely over a fixed Eulerian mesh, where the partial differential equations are solved (see Figure 3).
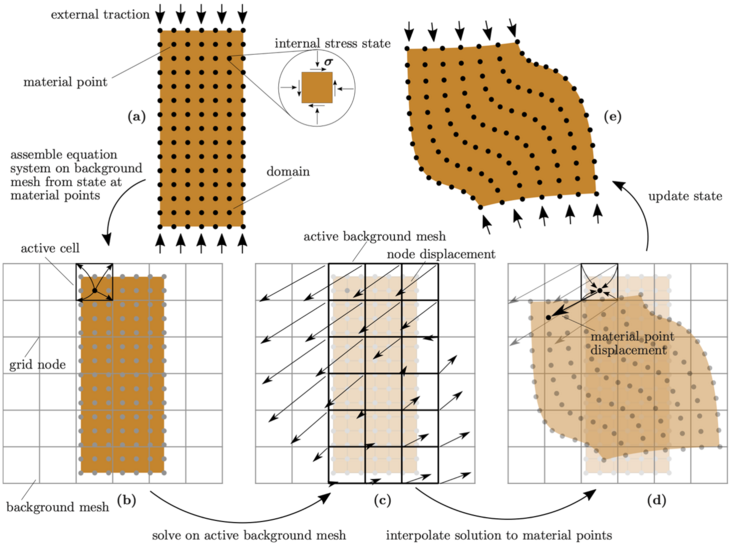
Figure 3: Illustrative description of the MPM (cf. Neuner et al. [3])
The overall goal of this research is to further develop such meshfree particle methods to establish a stable and robust numerical framework for solving large deformation problems in generalized continua. To achieve this, a project is funded by the FWF (FWF 10.55776/PAT1342523), focusing on the further development and application of the MPM to generalized continua.
References:
[1] M. Neuner, R. A. Regueiro, and C. Linder (2022). “A Unified Finite Strain Gradient-Enhanced Micropolar Continuum Approach for Modeling Quasi-Brittle Failure of Cohesive-Frictional Materials”. In: International Journal of Solids and Structures 254–255, p. 111841.
[2] M. Neuner, S. Abrari Vajari, P. K. Arunachala, and C. Linder (2022). “A Better Understanding of the Mechanics of Borehole Breakout Utilizing a Finite Strain Gradient-Enhanced Micropolar Continuum Model”. In: Computers and Geotechnics, p. 105064.
[3] M. Neuner, A. Dummer, S. Abrari Vajari, P. Gamnitzer, H. Gimperlein, C. Linder, G. Hofstetter (2024). “A B-spline based gradient-enhanced micropolar implicit material point method for large localized inelastic deformations”. In: Computer Methods in Applied Mechanics and Engineering 431
