Numerical and experimental investigations on creeping slopes
Wider research context: Giant slow-moving landslides occur worldwide in mechanically weak stratum and are sensitive to hydrological forcing, especially in climate change scenarios. They may creep slowly with slide masses slipping a few centimetres to a few metres each year and can accelerate to fail catastrophically, resulting in destruction and casualties. However, the mechanisms regulating the slow-to-fast transition toward their catastrophic collapse in the in-situ scale remain elusive. As a result, the prediction of the long-term motion of creeping landslides and transient response to hydrologic triggers relies largely on simplified models based on in-situ monitoring observations and on viscous rheology, while the dynamic coupling of time effects and matric suction in landslides under the time-variable hydrologic boundary conditions is often omitted.
Objectives: In this project, we will explore the slow-to-fast transition of a slow-moving landslide in partially saturated state and develop a numerical model to describe the creeping movement of landslides, including slow-to-fast transition of creep under time-variable hydraulic conditions.
Approach: A slow-moving landslide (Fig.1) instrumented with advanced monitoring networks will be chosen as a case to study the effects of external forcing, e.g. rainfall, underground water table change, water level fluctuation at the toe etc., on its slow motion; In-situ creep tests (Fig.2) and centrifuge model tests will be employed to study the long-term deformation of shear zone soils; A numerical model with an advanced constitutive model, incorporating the effects of time and suction, will be developed to predict the slow-motion under time-dependent hydrologic conditions.
Level of originality: An important innovation is the constitutive model, considering effects of time and suction, for clastic landslide soils. The evolution equation for suction links to saturation degree under time-variable hydrologic conditions during slow deformation. Moreover, the total stress is decomposed into a non-Newtonian-like viscous stress and a Coulomb-like friction stress. In this way, the transition between slow-moving behaviour (Coulomb stress dominance) and fast-moving behaviour (non-Newtonian stress dominance) can be described.
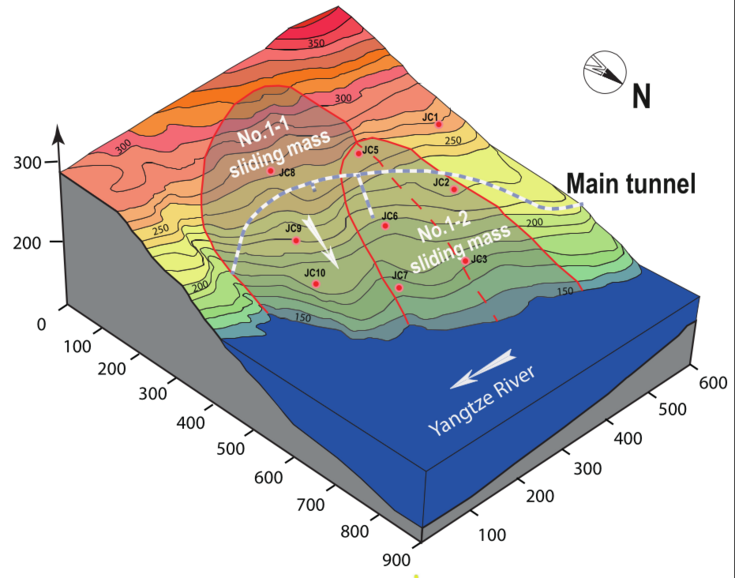
Fig.1 3D view of the Huangtupo landslide

Fig.2 In-situ creep tests in the slow-moving landslide
