Weiterentwicklung netzfreier Partikelmethoden
Weiterentwicklung netzfreier Partikelmethoden für die Analyse großer Deformationen in verallgemeinerten Kontinua
Die Beschreibung des Versagens von quasi-spröden Materialien ist eine herausfordernde Aufgabe in der numerischen Mechanik. Während klassische Kontinuumsmodelle – üblicherweise basierend auf entfestigender Plastizität, Schädigungsmechanik oder deren Kombination – grundsätzlich in der Lage sind, ein solches Versagen abbzubilden, leiden sie unter einem Mangel an Objektivität, was zu einem Verlust der Elliptizität der zugrunde liegenden Differentialgleichungen führt. Dies wiederum führt zur Lokalisierung der Verzerrungen in die kleinst mögliche Domäne, d.h., einer einzelnen Elementsreihe in Finite-Elemente-Simulationen, was zu einer Netzabhängigkeit bzw. nicht-konvergentem numerischen Verhalten führt.
Um eine stabile und robuste Formulierung von Materialmodellen zu gewährleisten, ist eine entsprechende Regularisierung des entfestigenden Verhaltens erforderlich. Die Verwendung verallgemeinerter Kontinua, wie etwa gradienten-erweiterter, Cosserat- oder mikromorpher Kontinua, stellt eine nachgewiesene effiziente Methode zur Regularisierung dar und führt so zu netzunabhängigen Ergebnissen in numerischen Simulationen (siehe Abbildung 1).
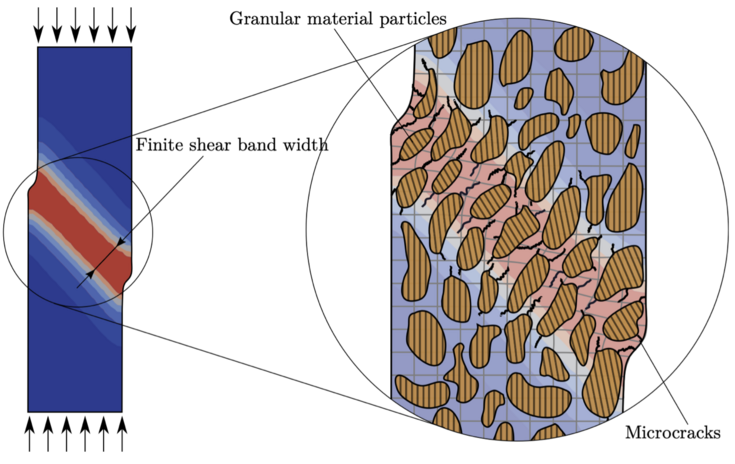
Abbildung 1: Berechnetes Scherband eines quasi-spröden Materials mit einem gradienten-erweiterten mikropolaren Schädigungs-Plastizitätsmodells unter Berücksichtigung großer Verformungen (vgl. Neuner et al. [1]).
Allerdings werden durch lokalisierte Versagensverhalten von Natur aus große Verformungen im Versagensbereich induziert, was bei der Anwendung von Lagrangen Finite-Elemente-Methoden zu übermäßigen Netzverzerrungen führt (siehe Abbildung 2).
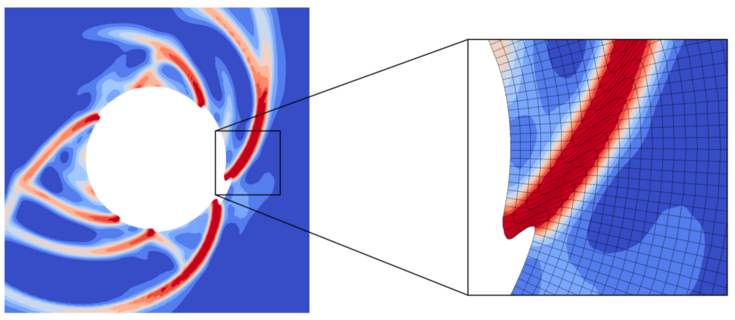
Abbildung 2: Berechnete Schädigungsverteilung eines Bohrloch Ausbruchs, unter Verwendung eines gradienten-erweiterten mikropolaren Schädigungs-Plastizitätsmodells für Sandstein unter Anwendung der klassischen Finite-Elemente-Methode (vgl. Neuner et al. [2]).
Netzfreie Partikelmethoden, wie die Partikel-Finite-Elemente-Methode (PFEM), die Diskrete-Elemente-Methode (DEM), Glattpartikel-Hydrodynamik (SPH), die Reproduzierende Kernel-Partikel-Methode (RKPM) und die Materialpunktsmethode (MPM), haben sich als geeignete Alternativen zur Lösung von Problemen mit großen Verformungen erwiesen.
Dahingehend wurde kürzlich in Neuner et al. [3] erfolgreich eine auf B-Splines basierende implizite MPM auf verallgemeinerte Kontinua zur Modellierung großer lokalisierter Verformungen angewandt. Im Gegensatz zur Lagrangen Finite-Elemente-Methode, wird in der MPM die Geometrie mit Partikeln diskretisiert, welche sich frei über ein festes Eulersches Netz bewegen, auf dem wiederum die partiellen Differentialgleichungen gelöst werden (siehe Abbildung 3).
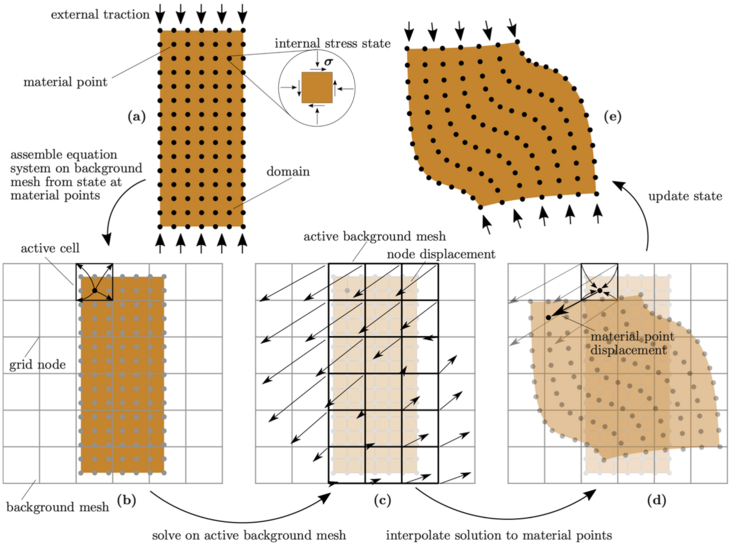
Abbildung 3: Illustrative Darstellung der MPM (vgl. Neuner et al. [3]).
Das übergeordnete Ziel dieser Forschung ist es, solche netzfreien Partikelmethoden weiterzuentwickeln um eine stabile und robuste numerisches Methode zur Lösung von Problemen mit großen Verformungen in verallgemeinerten Kontinua zu etablieren. Um dies zu erreichen, hat der FWF ein Projekt gefördert (FWF 10.55776/PAT1342523), welches sich auf die Weiterentwicklung und Anwendung der MPM auf verallgemeinerte Kontinua fokusiert.
Referenzen:
[1] M. Neuner, R. A. Regueiro, and C. Linder (2022). “A Unified Finite Strain Gradient-Enhanced Micropolar Continuum Approach for Modeling Quasi-Brittle Failure of Cohesive-Frictional Materials”. In: International Journal of Solids and Structures 254–255, p. 111841.
[2] M. Neuner, S. Abrari Vajari, P. K. Arunachala, and C. Linder (2022). “A Better Understanding of the Mechanics of Borehole Breakout Utilizing a Finite Strain Gradient-Enhanced Micropolar Continuum Model”. In: Computers and Geotechnics, p. 105064.
[3] M. Neuner, A. Dummer, S. Abrari Vajari, P. Gamnitzer, H. Gimperlein, C. Linder, G. Hofstetter (2024). “A B-spline based gradient-enhanced micropolar implicit material point method for large localized inelastic deformations”. In: Computer Methods in Applied Mechanics and Engineering 431
