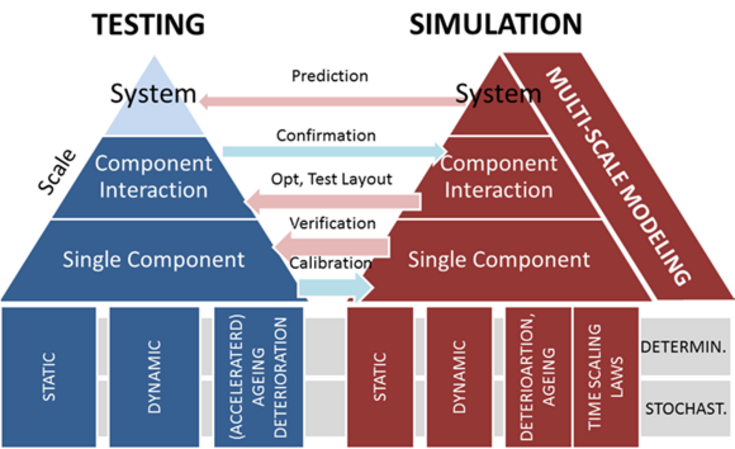
The life time performance of traditional fastening systems, as well as new future products, is determined by the performance of every single component and their interaction. Depending on the type of system, the base material can range from concrete or masonry to e.g. drywall. The anchor itself can be made from various metals or plastics and carry loads due to friction, shape interlock or adhesive glues. As shown in Figure both testing and simulation have to cover the behavior of single components, then their interaction and finally characterize the system behavior. This multi-scale problem can be numerically overcome by multi-scale modeling concepts, such as coarse graining or homogenization [1].
Over the years significant progress was made in accurately modeling single components based on extensive experimental investigations, see e.g. [2]. In addition to traditional continuum based elastic or elastic-plastic models, a broad range of continuum damage models as well as discrete models were developed, which mostly use a finite element or finite difference formulation. The former comprise crack-band models [3], non-local damage models [4, 5] but also microplane models [6, 7]. Typical examples for discrete models are e.g. lattice type particle models [8, 9].
Many studies were concerned with deterministic models to describe the load carrying capacity mostly under static short term loads. Similarly, modeling the component interaction was studied for certain problems. Modeling components under dynamic load on the other side was for some time neglected and only recently has become a focus of interest [10, 11]. Adequate stochastic models that can account for the true form of correlation between, and distribution of random variables are so far missing. In most research and codes simplifications are made by resorting to normally distributed variables and linear correlation, if at all considered. This approach unfortunately does not necessarily lie on the safe side and needs improvement.